Spesso sentiamo dire che un mercato e/o strumento finanziario è molto volatile, ma…che cosa significa?
Significa che i prezzi hanno grandi oscillazioni sia al rialzo sia al ribasso.
La volatilità, infatti, misura l’incertezza circa i movimenti futuri dei prezzi di un investimento: al crescere della volatilità, aumenta la probabilità che la performance risulti molto elevata o molto bassa.
Per calcolare la volatilità si utilizza la Deviazione Standard, un indice statistico che misura la quantità di variabilità o di dispersione attorno alla media.
Vediamo in parole semplici cosa significa. Si prende una serie storica di rendimenti di uno strumento finanziario. Da qui si ricava il rendimento medio, quindi si calcola quanto si discostano i rendimenti in più o in meno dal rendimento medio. Il calcolo da fare è:
σ = √(R1-Rm)²+(R2-Rm)²+(R3-Rm)²+…+(Rn-Rm)²
—————————————————–
n
σ = Deviazione Standard
R1 = rendimento 1
R2 = rendimento 2
Rm = Rendimento medio
n = numero di rilevazioni del rendimento
radice quadrata della somma dei quadrati delle differenze tra i vari rendimenti e il rendimento medio diviso il numero di osservazioni del rendimento.
Facciamo un esempio. Prendiamo uno strumento finanziario che realizzato le seguenti performance annuali:
R1 = 13%
R2 = 11%
R3 = 15%
R4 = 12%
R5 = 9%
R6 = 6%
Rm = (13+11+15+12+9+6)/6 = 66/6 = 11%
adesso calcoliamo la Deviazione Standard con la formula:
σ = √((13-11)²+(11-11)²+(15-11)²+(12-11)²+(9-11)²+(6-11)²)/6 =
√((2)²+(0)²+(4)²+(1)²+(-2)²+(-5)²)/6 = √(4+0+16+1+4+25)/6 =
√50/6 = √8,33 = 2,886%
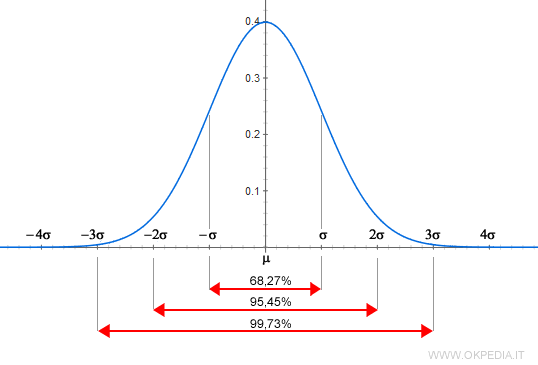
Quando conosciamo il rendimento medio di uno strumento finanziario e la sua deviazione standard, statisticamente:
Più è alta la deviazione standard e quindi la volatilità, più i rendimenti saranno differenti dal rendimento medio: lo strumento finanziario è più rischioso.
Contattami per approfondire questo o altri argomenti
